前言
咱们先来看两个问题:
第一个问题来自编程之美上,Tango是微软亚洲研究院的一个试验项目,如图1所示。研究院的员工和实习生们都很喜欢在Tango上面交流灌水。传说,Tango有一大“水王”,他不但喜欢发帖,还会回复其他ID发的每个帖子。坊间风闻该“水王”发帖数目超过了帖子总数的一半。如果你有一个当前论坛上所有帖子(包括回帖)的列表,其中帖子作者的ID也在表中,你能快速找出这个传说中的Tango水王吗?
图1 Tango

图2 谷歌中搜索关键字“结构之法”
第二十一章、发帖水王及其扩展
第一节、74.数组中超过出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
分析:编程之美上也有这道题,不过它变换了题目的表述形式,即是如本文前言所述的寻找发帖水王的问题。
ok,咱们来解决上述这道题,以微软面试100题第74题的阐述为准(本程序员编程艺术系列就是按照之前整理的微软100题一题一题展开而来的)。
一个数组中有很多数,现在我们要找出这个数组中那个超过出现次数一半的数字,怎么找呢?大凡当我们碰到某一个杂乱无序的东西时,我们人的内心本质期望是希望把它梳理成有序的。所以,我们得分两种情况来讨论,无序和有序:
- 如果无序,那么我们是不是可以先把数组中所有这些数字先进行排序,至于选取什么排序方法则不在话下,最常用的快速排序O(N*logN)即可。排完序呢,直接遍历。在遍历整个数组的同时统计每个数字的出现次数,然后把那个出现次数超过一半的数字直接输出,题目便解答完成了。总的时间复杂度为O(N*logN+N)。
- 但各位再想想,如果是有序的数组呢或者经过上述由无序的数组变成有序后的数组呢?是否在排完序O(N*logN)后,真的还需要再遍历一次整个数组么?我们知道,既然是数组的话,那么我们可以根据数组索引支持直接定向到某一个数。我们发现,一个数字在数组中的出现次数超过了一半,那么在已排好序的数组索引的N/2处(从零开始编号),就一定是这个数字。自此,我们只需要对整个数组排完序之后,然后直接输出数组中的第N/2处的数字即可,这个数字即是整个数组中出现次数超过一半的数字,总的时间复杂度由于少了最后一次整个数组的遍历,缩小到O(N*logN)。
- 然不论是上述思路一的O(N*logN+N),还是思路二的O(N*logN),时间复杂度并无本质性的改变。我们需要找到一种更为有效的思路或方法。既要缩小总的时间复杂度,那么就用查找时间复杂度为O(1),事先预处理时间复杂度为O(N)的hash表。哈希表的键值(Key)为数组中的数字,值(Value)为该数字对应的次数。然后直接遍历整个hash表,找出每一个数字在对应的位置处出现的次数,输出那个出现次数超过一半的数字即可。
- Hash表需要O(N)的开销空间,且要设计hash函数,还有没有更好的办法呢?我们可以试着这么考虑,如果每次删除两个不同的数(不管是不是我们要查找的那个出现次数超过一半的数字),那么,在剩下的数中,我们要查找的数(出现次数超过一半)出现的次数仍然超过总数的一半。通过不断重复这个过程,不断排除掉其它的数,最终找到那个出现次数超过一半的数字。这个方法,免去了上述思路一、二的排序,也避免了思路三空间O(N)的开销,总得说来,时间复杂度只有O(N),空间复杂度为O(1),不失为最佳方法。
或许,你还没有明白上述思路4的意思,举个简单的例子吧,如数组a[5]={0,1,2,1,1};
很显然,若我们要找出数组a中出现次数超过一半的数字,这个数字便是1,若根据上述思路4所述的方法来查找,我们应该怎么做呢?通过一次性遍历整个数组,然后每次删除不相同的两个数字,过程如下简单表示:
0 1 2 1 1 =>2 1 1=>1,最终,1即为所找。
但是如果是5,5,5,5,1,还能运用上述思路么?额,别急,请看下文思路5。
5. 咱们根据数组的特性进一步考虑@zhedahht: 数组中有个数字出现的次数超过了数组长度的一半。也就是说,有个数字出现的次数比其他所有数字出现次数的和还要多。
因此我们可以考虑在遍历数组的时候保存两个值:一个是数组中的一个数字,一个是次数。当我们遍历到下一个数字的时候,如果下一个数字和我们之前保存的数字相同,则次数加1。 如果下一个数字和我们之前保存的数字不同,则次数减1。如果次数为零,我们需要保存下一个数字,并把次数重新设为1。下面,举二个例子:
- 第一个例子,5,5,5,5,1 :
不同的相消,相同的累积。遍历到第四个数字时,candidate 是5, nTimes 是4; 遍历到第五个数字时,candidate 是5, nTimes 是3; nTimes不为0,那么candidate就是超过半数的。
- 第二个例子,0,1,2,1,1:
开始时,保存candidate是数字0,ntimes为1,遍历到数字1后,与数字0不同,则ntime减1变为零,;接下来,遍历到数字2,2与1不同,candidate保存数字2,且ntimes重新设为1;继续遍历到第4个数字1时,与2不同,ntimes减一为零,同时candidate保存为1;最终遍历到最后一个数字还是1,与我们之前candidate保存的数字1相同,ntime加一为1。最后返回的是之前保存的candidate为1。
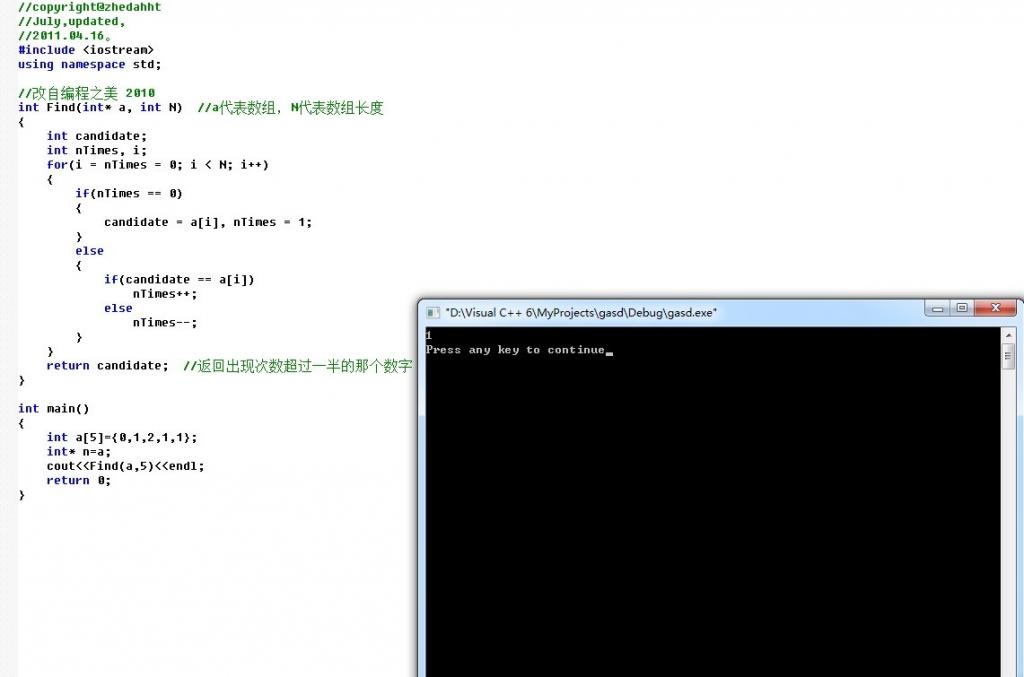
针对上述程序,我再说详细点,0,1,2,1,1:
- i=0,candidate=0,nTimes=1;
- i=1,a[1]=0 != candidate,nTimes--,=0;
- i=2,candidate=2,nTimes=1;
- i=3,a[3] != candidate,nTimes--,=0;
- i=4,candidate=1,nTimes=1;
- 如果是0,1,2,1,1,1的话,那么i=5,a[5]=1=candidate,nTimes++,=2;......
Ok,思路清楚了,完整的代码如下:
- //改自编程之美 2010
- Type Find(Type* a, int N) //a代表数组,N代表数组长度
- {
- Type candidate;
- int nTimes, i;
- for(i = nTimes = 0; i < N; i++)
- {
- if(nTimes == 0)
- {
- candidate = a[i], nTimes = 1;
- }
- else
- {
- if(candidate == a[i])
- nTimes++;
- else
- nTimes--;
- }
- }
- return candidate;
- }
或者:
- //copyright@zhedahht
- //July,updated,
- //2011.04.16。
- #include <iostream>
- using namespace std;
- bool g_Input = false;
- int Num(int* numbers, unsigned int length)
- {
- if(numbers == NULL && length == 0)
- {
- g_Input = true;
- return 0;
- }
- g_Input = false;
- int result = numbers[0];
- int times = 1;
- for(int i = 1; i < length; ++i)
- {
- if(numbers[i] == result)
- times++;
- else
- times--;
- if(times == 0)
- {
- result = numbers[i];
- times = 1;
- }
- }
- //检测输入是否有效。
- times = 0;
- for(i = 0; i < length; ++i)
- {
- if(numbers[i] == result)
- times++;
- }
- if(times * 2 <= length)
- //检测的标准是:如果数组中并不包含这么一个数字,那么输入将是无效的。
- {
- g_Input = true;
- result = 0;
- }
- return result;
- }
- int main()
- {
- int a[10]={1,2,3,4,6,6,6,6,6};
- int* n=a;
- cout<<Num(a,9)<<endl;
- return 0;
- }
这段代码与上段代码本质上并无二致,不过有几个问题,还是需要我们注意:
- 当输入无效性时,要处理。比如数组长度为0。
- 最后,上述代码加了一个判断,如果数组中并不包含这么一个数字,那么输入也是无效的。因此在函数结束前还加了一段代码来验证输入是不是有效的。
第二节、加强版水王:找出出现次数刚好是一半的数字
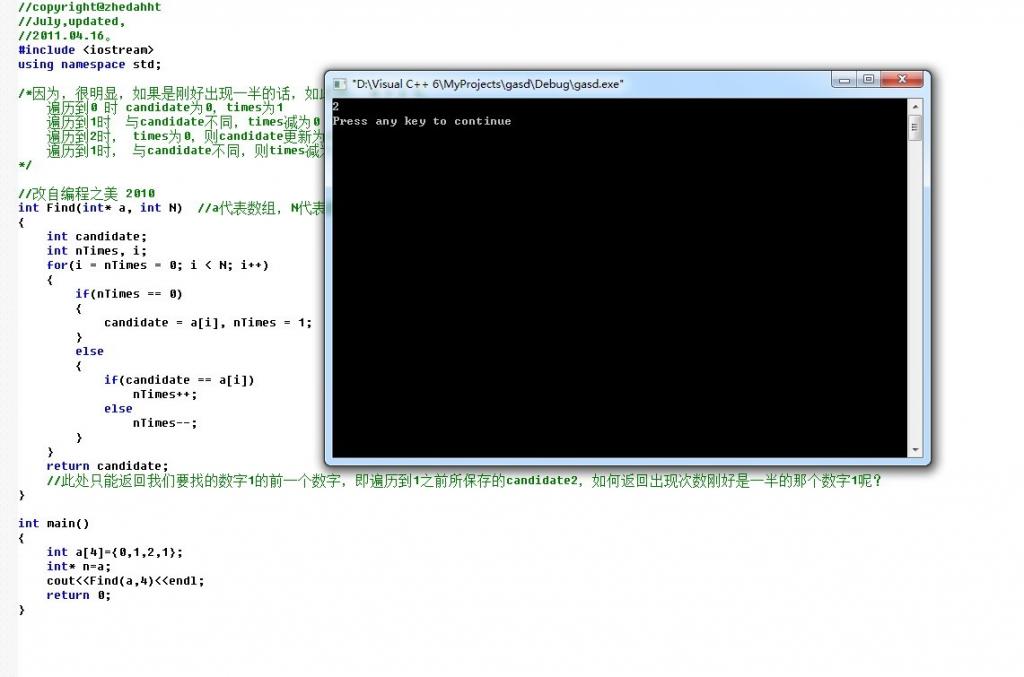
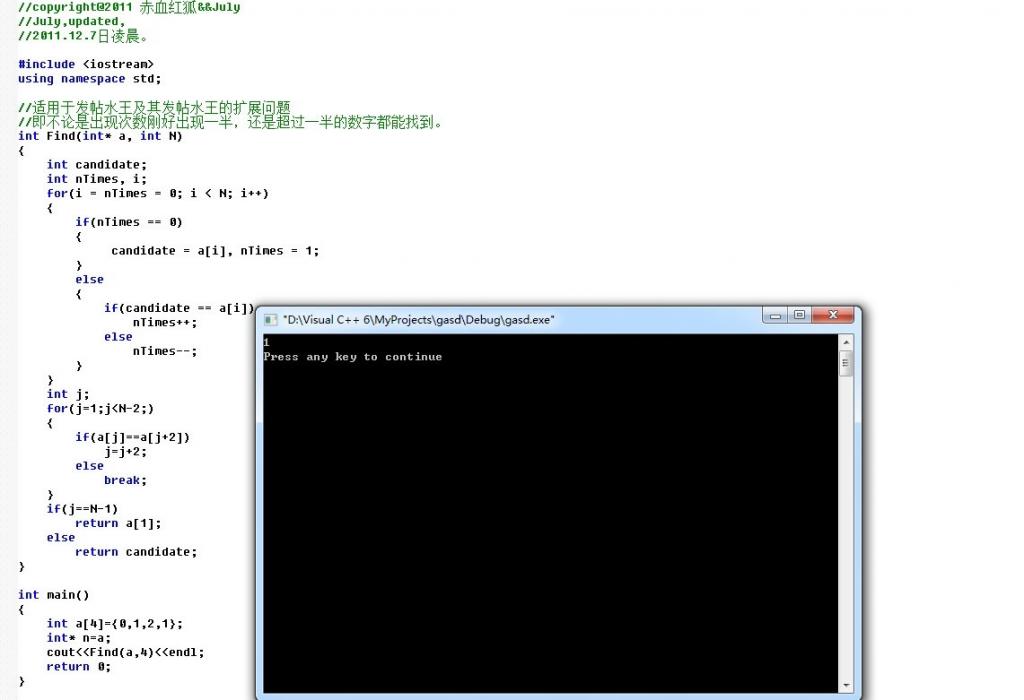
2、bug出现!
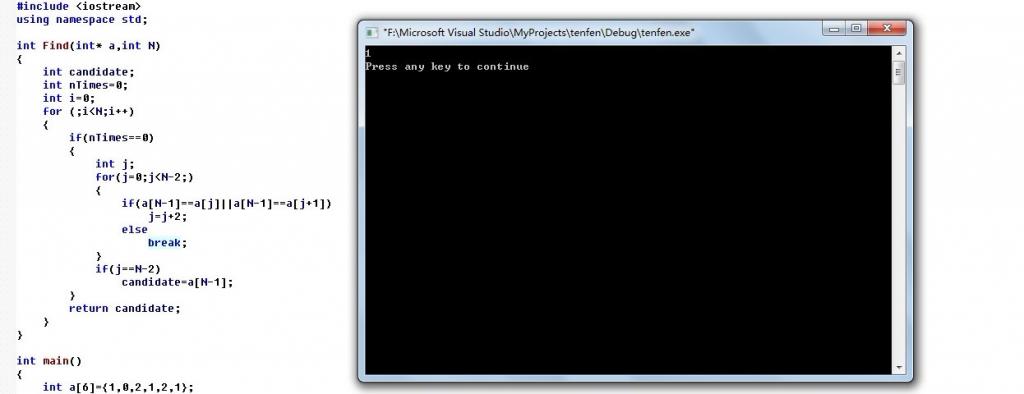
3、持续改进
- #include<iostream>
- using namespace std;
- int Find(int* a, int N)
- {
- int candidate1,candidate2;
- int nTimes1, nTimes2, i;
- for(i = nTimes1 = nTimes2 =0; i < N; i++)
- {
- if(nTimes1 == 0)
- {
- candidate1 = a[i], nTimes1 = 1;
- }
- else if(nTimes2 == 0 && candidate1 != a[i])
- //注意:这里的判断条件加上第二个变量是否等于第一个变量的判断
- {
- candidate2 = a[i], nTimes2 = 1;
- }
- else
- {
- if(candidate1 == a[i])
- nTimes1++;
- else if(candidate2 == a[i])
- nTimes2++;
- else
- {
- nTimes1--;
- nTimes2--;
- }
- }
- }
- return nTimes1>nTimes2?candidate1:candidate2;
- }
- int main()
- {
- int a[4]={0,1,2,1};
- cout<<Find(a,4)<<endl;
- // int a[6]={1,0,2,1,2,1};
- // cout<<Find(a,6)<<endl;
- }
4、读者反馈
- int Find(int* a, int N) //a代表数组,N代表数组长度
- {
- int candidate;
- int nTimes, i;
- for(i = nTimes = 0; i < N; i++)
- {
- if(nTimes == 0)
- {
- candidate = a[i], nTimes = 1;
- }
- else
- {
- if(candidate == a[i])
- nTimes++;
- else
- nTimes--;
- }
- }
- int cTimes = 0;
- int candidate2 = a[N-1];
- for(i = 0; i < N; i ++)
- {
- if(a[i] == candidate)
- {
- cTimes++;
- }
- }
- return cTimes == N/2 ? candidate : candidate2;
- }
- int MoreThanHalf(int a[], int N)
- {
- int sum1 = 0;//最后一个元素的个数
- int sum2 = 0;
- int candidate;
- int i;
- for(i=0;i<N-1;i++)//扫描前N-1个元素
- {
- if(a == a[N-1])//判断当前元素与最后一个是否相等
- sum1++;
- if(sum2 == 0)
- {
- candidate = a;
- sum2++;
- }
- else
- {
- if(a == candidate)
- sum2++;
- else
- sum2--;
- }
- }
- if((sum1+1) == N/2)
- return a[N-1];
- else
- return candidate;
- }
第二十二章、最短摘要的生成
Alibaba笔试题:给定一段产品的英文描述,包含M个英文字母,每个英文单词以空格分隔,无其他标点符号;再给定N个英文单词关键字,请说明思路并编程实现方法
String extractSummary(String description,String[] key words)
目标是找出此产品描述中包含N个关键字(每个关键词至少出现一次)的长度最短的子串,作为产品简介输出。(不限编程语言)20分。
这题是来自此篇文章中整理的阿里巴巴的笔试题,之前已经给出了这样一种思路,如下:
@owen:扫描过程始终保持一个[left,right]的range,初始化确保[left,right]的range里包含所有关键字则停止。然后每次迭代:
- 试图右移动left,停止条件为再移动将导致无法包含所有关键字。
- 比较当前range's length和best length,更新最优值。
- 右移right,停止条件为使任意一个关键字的计数+1。
- 重复迭代。
在那篇文章中也提到了编程之美有最短摘要生成的问题,与此问题类似。下面,我将介绍这种方法。首先,咱们来看一个问题。读者可以在百度或谷歌中搜索本博客名称的前4个字,”结构之法“,便会在第一个搜索结果中看到如下图所示的搜索项:
上图中,那段大致介绍本博客结构之法算法之道的文字:”程序员面试、算法研究、编程艺术、红黑树4大经典原创系列集锦与总结 作者:July--结构之法算法之道blog之博主。时间:2010年10月-2011年6月。出处:http://...“这段介于搜索关键词与最底下的URL便是我们所称之为的摘要。那么,这段摘要是怎么产生的呢?可以对问题进行如下的简化。
- 假设给定的已经是经过网页分词之后的结果,词语序列数组为W。其中W[0], W[1],…, W[N]为一些已经分好的词语。
- 假设用户输入的搜索关键词为数组Q。其中Q[0], Q[1],…, Q[m]为所有输入的搜索关键词。
这样,生成的最短摘要实际上就是一串相互联系的分词序列。比如从W[i]到W[j],其中,0<i<j<=N。例如上图所示的摘要“程序员面试、算法研究、编程艺术、红黑树4大经典原创吸了集锦与总结 作者:July--结构之法算法之道blog之博主.....”中包含了关键字——“结构之法”。
那么,我们该怎么做呢?
思路一:
在分析问题之前,先通过一个实际的例子来探讨。比如在本博客第一篇置顶文章的开头,有这么一段话:
“程序员面试、算法研究、编程艺术、红黑树4大经典原创系列集锦与总结
作者:July--结构之法算法之道blog之博主。时间:2010年10月-2011年6月。出处:http://blog.csdn.net/v_JULY_v。声明:版权所有,侵犯必究。”那么,我们可以猜想一下可能的分词结果:
”程序员/面试/、/算法/研究/、/编程/艺术/、/红黑树/4/大/经典/原创/系列/集锦/与/总结/ /作者/:/July/--/结构/之/法/算法/之/道/blog/之/博主/....“ (网页的分词效果W数组)
这也就是我们期望的W数组序列。
之前的Q数组序列为:
“结构之法”(用户输入的关键字Q数组)
再看下下面这个W-Q序列:
w0,w1,w2,w3,q0,w4,w5,q1,w6,w7,w8,q0,w9,q1
上述序列上面的是W数组(经过网页分词之后的结果),W[0], W[1],…, W[N]为一些已经分好的词语,
上述序列下面的是Q数组(用户输入的搜索关键词)。其中Q[0], Q[1],…, Q[m]为所有输入的搜索关键词。
ok,如果你不甚明白,我说的通俗点:如上W-Q序列中,我们可以把,q0,w4,w5,q1作为摘要,q0,w9,q1的也可以作为摘要,同样都包括了所有的关键词q0,q1,那么选取哪个是最短摘要呢?答案很明显,后一个更短,选取q0,w9,q1的作为最短摘要,这便是最短摘要的生成。
我们可以进一步可以想象,如下:
从用户的角度看:当我们在百度的搜索框中输入“结构之法”4个字时,搜索引擎将在索引数据库中(关于搜索引擎原理的大致介绍,可参考本博客中这篇文章:搜索引擎技术之概要预览)查找和匹配这4个字的网页,最终第一个找到了本博客的置顶的第一篇文章:[置顶]程序员面试、算法研究、编程艺术、红黑树4大系列集锦与总结;
从搜索引擎的角度看:搜索引擎经过把上述网页分词后,便得到了上述的分词效果,然后在这些分词中查找“结构之法”4个关键字,但这4个关键字不一定只会出现一遍,它可能会在这篇文章中出现多次,就如上面的W-Q序列一般。咱们可以假想出下面的结果(结构之法便出现了两次):
“程序员/面试/、/算法/研究/、/编程/艺术/、/红黑树/4/大/经典/原创/系列/集锦/与/总结/ /作者/:/July/--/结构/之/法/算法/之/道/blog/之/博主/././././转载/请/注明/出处/:/结构/之/法/算法/之/道/CSDN/博客/./././.”
由此,我们可以得出解决此问题的思路,如下:
- 从W数组的第一个位置开始查找出一段包含所有关键词数组Q的序列(第一个位置”程“开始:程序员/面试/、/算法/研究/、/编程/艺术/、/红黑树/4/大/经典/原创/系列/集锦/与/总结/ /作者/:/July/--/结构/之/法/查找包含关键字“结构之法”所有关键词的序列)。计算当前的最短长度,并更新Seq数组。
- 对目标数组W进行遍历,从第二个位置开始,重新查找包含所有关键词数组Q的序列(第二个位置”序“处开始:程序员/面试/、/算法/研究/、/编程/艺术/、/红黑树/4/大/经典/原创/系列/集锦/与/总结/ /作者/:/July/--/结构/之/法/查找包含关键字”结构之法“所有关键词的序列),同样计算出其最短长度,以及更新包含所有关键词的序列Seq,然后求出最短距离。
- 依次操作下去,一直到遍历至目标数组W的最后一个位置为止。
最终,通过比较,咱们确定如下分词序列作为最短摘要,即搜索引擎给出的分词效果:
”程序员面试、算法研究、编程艺术、红黑树4大经典原创系列集锦与总结 作者:July--结构之法算法之道blog之博主。时间:2010年10月-2011年6月。出处:http://...“
那么,这个算法的时间复杂度如何呢?
要遍历所有其他的关键词(M),对于每个关键词,要遍历整个网页的词(N),而每个关键词在整个网页中的每一次出现,要遍历所有的Seq,以更新这个关键词与所有其他关键词的最小距离。所以算法复杂度为:O(N^2 * M)。
思路二:
我们试着降低此问题的复杂度。因为上述思路一再进行查找的时候,总是重复地循环,效率不高。那么怎么简化呢?先来看看这些序列:
w0,w1,w2,w3,q0,w4,w5,q1,w6,w7,w8,q0,w9,q1
问题在于,如何一次把所有的关键词都扫描到,并且不遗漏。扫描肯定是无法避免的,但是如何把两次扫描的结果联系起来呢?这是一个值得考虑的问题。
沿用前面的扫描方法,再来看看。第一次扫描的时候,假设需要包含所有的关键词,从第一个位置w0处将扫描到w6处:
w0,w1,w2,w3,q0,w4,w5,q1,w6,w7,w8,q0,w9,q1
那么,下次扫描应该怎么办呢?先把第一个被扫描的位置挪到q0处。
w0,w1,w2,w3,q0,w4,w5,q1,w6,w7,w8,q0,w9,q1
然后把第一个被扫描的位置继续往后面移动一格,这样包含的序列中将减少了关键词q0。那么,我们便可以把第二个扫描位置往后移,这样就可以找到下一个包含所有关键词的序列。即从w4扫描到w9处,便包含了q1,q0:
w0,w1,w2,w3,q0,w4,w5,q1,w6,w7,w8,q0,w9,q1
这样,问题就和第一次扫描时碰到的情况一样了。依次扫描下去,在w中找出所有包含q的序列,并且找出其中的最小值,就可得到最终的结果。编程之美上给出了如下参考代码:
//July、updated,2011.10.21。
- int nTargetLen = N + 1; // 设置目标长度为总长度+1
- int pBegin = 0; // 初始指针
- int pEnd = 0; // 结束指针
- int nLen = N; // 目标数组的长度为N
- int nAbstractBegin = 0; // 目标摘要的起始地址
- int nAbstractEnd = 0; // 目标摘要的结束地址
- while(true)
- {
- // 假设未包含所有的关键词,并且后面的指针没有越界,往后移动指针
- while(!isAllExisted() && pEnd < nLen)
- {
- pEnd++;
- }
- // 假设找到一段包含所有关键词信息的字符串
- while(isAllExisted())
- {
- if(pEnd – pBegin < nTargetLen)
- {
- nTargetLen = pEnd – pBegin;
- nAbstractBegin = pBegin;
- nAbstractEnd = pEnd – 1;
- }
- pBegin++;
- }
- if(pEnd >= N)
- Break;
- }
小结:上述思路二相比于思路一,很明显提高了不小效率。我们在匹配的过程中利用了可以省去其中某些死板的步骤,这让我想到了KMP算法的匹配过程。同样是经过观察,比较,最后总结归纳出的高效算法。我想,一定还有更好的办法,只是我们目前还没有看到,想到,待我们去发现,创造。
思路三:
以下是读者jiaotao1983回复于本文评论下的反馈,非常感谢。
关于最短摘要的生成,我觉得July的处理有些简单,我以July的想法为基础,提出了自己的一些想法,这个问题分以下几步解决:
1,将传入的key words[]生成哈希表,便于以后的字符串比较。结构为KeyHash,如下:struct KeyHash{ int cnt; char key[]; int hash;}结构体中的hash代表了关键字的哈希值,key代表了关键字,cnt代表了在当前的扫描过程中,扫描到的该关键字的个数。当然,作为哈希表结构,该结构体中还会有其它值,这里不赘述。初始状态下,所有哈希结构的cnt字段为0。2,建立一个KeyWord结构,结构体如下:struct KeyWord{ int start; KeyHash* key; KeyWord* next; KeyWord* prev;}key字段指向了建立的一个KeyWord代表了当前扫描到的一个关键字,扫描到的多个关键字组成一个双向链表。start字段指向了关键字在文章中的起始位置。3,建立几个全局变量: KeyWord* head,指向了双向链表的头,初始为NULL。 KeyWord* tail,指向了双向链表的尾,初始为NULL。 int minLen,当前扫描到的最短的摘要的长度,初始为0。 int minStartPos,当前扫描到的最短摘要的起始位置。 int needKeyCnt,还需要几个关键字才能够包括全部的关键字,初始为关键字的个数。4,开始对文章进行扫描。每扫描到一个关键字时,就建立一个KeyWord的结构并且将其连入到扫描到的双向链表中,更新head和tail结构,同时将对应的KeyHash结构中的cnt加1,表示扫描到了关键字。如果cnt由0变成了1,表示扫描到一个新的关键字,因此needKeyCnt减1。5,当needKeyCnt变成0时,表示扫描到了全部的关键字了。此时要进行一个操作:链表头优化。
链表头指向的word是摘要的起始点,可是如果对应的KeyHash结构中的cnt大于1,表示扫描到的摘要中还有该关键字,因此可以跳过该关键字。因此,此时将链表头更新为下一个关键字,同时,将对应的KeyHash中的结构中的cnt减1,重复这样的检查,直至某个链表头对应的KeyHash结构中的cnt为1,此时该结构不能够少了。6,如果找到更短的minLength,则更新minLength和minStartPos。7,开始新一轮的搜索。此时摘除链表的第一个节点,将needKeyCnt加1,将下一个节点作为链表头,同样的开始链表头优化措施。搜索从上一次的搜索结束处开始,不用回溯。就是所,搜索在整个算法的过程中是一直沿着文章向下的,不会回溯。,直至文章搜索完毕。这样的算法的复杂度初步估计是O(M+N)。
8,另外,我觉得该问题不具备实际意义,要具备实际意义,摘要应该包含完整的句子,所以摘要的起始和结束点应该以句号作为分隔。这里,新建立一个结构:Sentence,结构体如下:struct Sentence{ int start; //句子的起始位置 int end; //句子的结束位置 KeyWord* startKey; //句子包含的起始关键字 KeyWord* endKey; //句子包含的结束关键字 Sentence* prev; //下一个句子结构 Sentence* next; //前一个句子结构}扫描到的多个句子结构组成一个链表。增加两个全局变量,分别指向了Sentence链表的头和尾。扫描时,建立关键字链表时,也要建立Sentence链表。当扫描到包含了所有的关键字时,必须要扫描到一个完整句子的结束。开始做Sentence头节点优化。做法是:查看Sentence结构中的全部key结构,如果全部的key对应的KeyHash结构的cnt属性全部大于1,表明该句子是多余的,去掉它,去掉它的时候更新对应的HashKey结构的关键字,因为减去了很多的关键字。然后对下一个Sentence结构做同样的操作,直至某个Sentence结构是必不可少的,就是说它包含了当前的摘要中只出现过一次的关键字!
扫描到了一个摘要后,在开始新的扫描。更新Sentence链表的头结点为下一个节点,同时更新对应的KeyHash结构中的cnt关键字,当某个cnt变成0时,就递增needKeycnt变量。再次扫描时仍然是从当前的结束位置开始扫描。初步估计时间也是O(M+N)。ok,留下一个编程之美一书上的扩展问题:当搜索一索一个词语后,有许多的相似页面出现,如何判断两个页面相似,从而在搜索结果中隐去这类结果?
本文参考:
- 编程之美第二章第2.3节寻找发帖水王;
- 编程之美第三章第3.5节最短摘要的生成;
- 。
后记
编程艺术系列从今年4月开始创作,已写了二十二章。此系列最初是我一个人写,后来我的一些朋友加入进来了,便成立了程序员编程艺术室,是我和一些朋友们一起写了,但到如今一直在坚持的又只剩下自己了。近些天,常常发呆胡乱思考一些东西,如个人写博刚过一年,有时候也看得一些有关互联网创业的文章,便有了下面写博VS创业这个话题:
- 读者第一(用户至上);
- 站在读者角度和思维方式阐述问题,文不易懂死不休(重视用户体验,用户不喜欢不会用的产品便是废品);
- 只写和创作读者最最需要的文章,东西(别人不需要,便没有市场,没有市场,一切免谈);
- 写博贵在坚持(创业贵在坚持)。
编程艺术系列一如之前早已说过,“因为编程艺术系列最后可能要写到第六十章”(语出自:--面试、算法、编程)。期待,编程艺术室的朋友能早日继续加入共同创作。以诸君为傲。ok,若有任何问题,欢迎随时不吝指正。转载请注明出处。完。July、2011.10。